Что значит система не определена. Матричная форма записи систем линейных алгебраических уравнений. Пусть система имеет решение. Покажем, что

Раздел 5. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Системы линейных уравнений

Основные понятия

Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида

где числа а ij , i =
, j = называются коэффициентами системы, числа b i – свободными членами. Подлежат нахождению числа х п .

Такую систему удобно записывать в компактной матричной форме
.

Здесь А – матрица коэффициентов системы, называемая основной матрицей :

–вектор-столбец из неизвестных х j , – вектор-столбец из свободных членовb i .

Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов

Решением системы называется п значений неизвестных х 1 =с 1 , х 2 =с 2 , ..., х п =с п , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .

Система уравнений называется совместной , если она имеет хотя бы одно решение, и несовместной , если она не имеет ни одного решения.

Совместная система называется определенной , если она имеет единственное решение, и неопределенной , если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или не совместна. Если система совместна, то найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной , если все свободные члены равны нулю:

Однородная система всегда совместна, так как х 1 =х 2 =…=х п =0 является решением системы. Это решение называется нулевым или тривиальным.

Решение систем линейных уравнений

Пусть дана произвольная система т линейных уравнений с п неизвестными

Теорема 1 (Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы.

Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.

П р и м е р. Исследовать на совместность систему

Решение.
,r (A )=1;
, r ()=2,
.

Таким образом, r (A) r (), следовательно, система несовместна.

Решение невырожденных систем линейных уравнений. Формулы Крамера

Пусть дана система п линейных уравнений с п неизвестными

или в матричной форме А∙Х=В.

Основная матрица А такой системы – квадратная. Определитель этой матрицы называется определителем системы . Если определитель системы отличен от нуля, то система называется невырожденной .

Найдем решение данной системы уравнений в случае ∆0. умножив обе части уравнения А∙Х=В слева на матрицу А  1 , получим А  1 ∙ А∙Х= А  1 ∙В. Поскольку А  1 ∙ А=Е и Е∙Х=Х, то Х= А  1 ∙ В. Данный способ решения системы называют матричным .

Из матричного способа вытекают формулы Крамера
, где ∆ – определитель основной матрицы системы, а ∆ i – определитель, полученный из определителя ∆ путем замены i -го столбца коэффициентов столбцом из свободных членов.

П р и м е р. Решить систему

Решение.
, 70,
,
. Значит,х 1 =, х 2 =
.

Решение систем линейных уравнений методом Гаусса

Метод Гаусса состоит в последовательном исключении неизвестных.

Пусть дана система уравнений

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному ) виду.

где k ≤ п, а ii  0, i = . Коэффициенты а ii называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

Замечания:

Если ступенчатая система оказывается треугольной, т.е. k = n , то исходная система имеет единственное решение. Из последнего уравнения находим х п , из предпоследнего уравнения находим х п  1 , далее поднимаясь по системе вверх, найдем все остальные неизвестные.

На практике удобнее работать с расширенной матрицей системы, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент а 11 был равен 1(уравнения переставить местами, либо разделить на а 11 1).

П р и м е р. Решить систему методом Гаусса

Решение. В результате элементарных преобразований над расширенной матрицей системы

~
~
~

исходная система свелась к ступенчатой:

Поэтому общее решение системы: x 2 =5 x 4  13 x 3  3; x 1 =5 x 4  8 x 3  1.

Если положить, например, х 3 =х 4 =0, то найдем одно из частных решений этой системы х 1 =  1, х 2 =  3, х 3 =0, х 4 =0.

Систем однородных линейных уравнений

Пусть дана система линейных однородных уравнений

Очевидно, что однородная система всегда совместна, она имеет нулевое (тривиальное) решение.

Теорема 4. Для того, чтобы система однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е. r < n .

Теорема 5. Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевое решение, необходимо и достаточно, чтобы определитель ее основной матрицы был равен нулю, т.е. ∆=0.

Если система имеет ненулевые решения, то ∆=0.

П р и м е р. Решить систему

Решение.
,r (A )=2
, п=3. Так как r < n , то система имеет бесконечное множество решений.

,
. Стало быть,х 1 ==2х 3 , х 2 ==3х 3 – общее решение.

Положив х 3 =0, получим одно частное решение: х 1 =0, х 2 =0, х 3 =0. Положив х 3 =1, получим второе частное решение: х 1 =2, х 2 =3, х 3 =1 и т.д.

Вопросы для контроля

Что такое система линейных алгебраических уравнений?

Поясните следующие понятия: коэффициент, свободный член, основная и расширенная матрицы.

Какими бывают системы линейных уравнений? Сформулируйте теорему Кронкера-Капелли (о совместности системы линейных уравнений).

Перечислите и поясните методы решения систем линейных уравнений.

где x * - один из решений неоднородной системы (2) (например (4)), (E−A + A) образует ядро (нуль пространство) матрицы A .

Сделаем скелетное разложение матрицы (E−A + A) :

E−A + A=Q·S

где Q n×n−r - матрица rank(Q)=n−r , S n−r×n -матрица rank(S)=n−r .

Тогда (13) можно записать в следующем виде:

x=x*+Q·k, ∀ k∈ R n-r .

где k=Sz .

Итак, процедура нахождения общего решения системы линейных уравнений с помощью псевдообратной матрицы можно представить в следующем виде:

Вычисляем псевдообратную матрицу A + .
Вычисляем частное решение неоднородной системы линейных уравнений (2): x *=A + b .
Проверяем совместность системы. Для этого вычисляем AA + b . Если AA + b ≠b , то система несовместна. В противном случае продолжаем процедуру.
Высисляем E−A + A.
Делаем скелетное разложение E−A + A=Q·S.
Строим решение

x=x*+Q·k, ∀ k∈ R n-r .

Решение системы линейных уравнений онлайн

Онлайн калькулятор позволяет найти обшее решение системы линейных уравнений с подробными объяснениями.

Однако на практике широко распространены еще два случая:

– Система несовместна (не имеет решений);
– Система совместна и имеет бесконечно много решений.

Примечание : термин «совместность» подразумевает, что у системы существует хоть какое-то решение. В ряде задач требуется предварительно исследовать систему на совместность, как это сделать – см. статью о ранге матриц .

Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса . На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников .

Сами элементарные преобразования матрицы – точно такие же , разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).

Пример 1

Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных , то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.

Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.

(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.

(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.

(4) К третьей строке прибавляем вторую строку.

Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: . Ясно, что так быть не может. Действительно, перепишем полученную матрицу обратно в систему линейных уравнений:

Если в результате элементарных преобразований получена строка вида , где – число, отличное от нуля, то система несовместна (не имеет решений) .

Как записать концовку задания? Нарисуем белым мелом: «в результате элементарных преобразований получена строка вида , где » и дадим ответ: система не имеет решений (несовместна).

Если же по условию требуется ИССЛЕДОВАТЬ систему на совместность, тогда необходимо оформить решение в более солидном стиле с привлечением понятия ранга матрицы и теоремы Кронекера-Капелли .

Обратите внимание, что здесь нет никакого обратного хода алгоритма Гаусса – решений нет и находить попросту нечего.

Пример 2

Решить систему линейных уравнений

Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».

Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же , как только появилась строка вида , где . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица . Матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет никакой необходимости, так как появилась строка вида , где . Следует сразу дать ответ, что система несовместна.

Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.

Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.

Пример 3

Решить систему линейных уравнений

Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.

Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Вот и всё, а вы боялись.

(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.

Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!

(2) Последние три строки пропорциональны, две из них можно удалить.

Здесь опять нужно проявить повышенное внимание , а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.

В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду:

При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.

Перепишем соответствующую систему уравнений:

«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки тоже нет. Значит, это третий оставшийся случай – система имеет бесконечно много решений. Иногда по условию нужно исследовать совместность системы (т.е. доказать, что решение вообще существует), об этом можно прочитать в последнем параграфе статьи Как найти ранг матрицы? Но пока разбираем азы:

Бесконечное множество решений системы коротко записывают в виде так называемого общего решения системы .

Общее решение системы найдем с помощью обратного хода метода Гаусса.

Сначала нужно определить, какие переменные у нас являются базисными , а какие переменные свободными . Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные .

Базисные переменные всегда «сидят» строго на ступеньках матрицы .
В данном примере базисными переменными являются и

Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: – свободные переменные.

Теперь нужно все базисные переменные выразить только через свободные переменные .

Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную :

Теперь смотрим на первое уравнение: . Сначала в него подставляем найденное выражение :

Осталось выразить базисную переменную через свободные переменные :

В итоге получилось то, что нужно – все базисные переменные ( и ) выражены только через свободные переменные :

Собственно, общее решение готово:

Как правильно записать общее решение?
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные следует записать на второй и четвертой позиции:
.

Полученные же выражения для базисных переменных и , очевидно, нужно записать на первой и третьей позиции:

Придавая свободным переменным произвольные значения , можно найти бесконечно много частных решений . Самыми популярными значениями являются нули, поскольку частное решение получается проще всего. Подставим в общее решение:

– частное решение.

Другой сладкой парочкой являются единицы, подставим в общее решение:

– еще одно частное решение.

Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)

Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение и подставьте его в левую часть каждого уравнения исходной системы:

Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.

Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.

Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение ?

Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае и , и подставить их в левую часть каждого уравнения системы.

В левую часть первого уравнения системы:

В левую часть второго уравнения системы:

Получена правая часть исходного уравнения.

Пример 4

Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание . Полное решение и ответ в конце урока.

И еще пара примеров для закрепления материала

Пример 5

Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения

Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.

Вот такая красота:

Базисные переменные сидят на ступеньках, поэтому – базисные переменные.
Свободная переменная, которой не досталось ступеньки здесь всего одна:

Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:

Рассмотрим второе уравнение и подставим в него найденное выражение :

Рассмотрим первое уравнение и подставим в него найденные выражения и :

Да, всё-таки удобен калькулятор, который считает обыкновенные дроби.

Таким образом, общее решение:

Еще раз, как оно получилось? Свободная переменная одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных , тоже заняли свои порядковые места.

Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)

Подставляем трех богатырей , , в левую часть каждого уравнения системы:

Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.

Теперь из найденного общего решения получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная . Ломать голову не нужно.

Пусть , тогда – частное решение.
Пусть , тогда – еще одно частное решение.

Ответ : Общее решение: , частные решения: , .

Зря я тут про негров вспомнил... ...потому что в голову полезли всякие садистские мотивы и вспомнилась известная фотожаба, на которой куклуксклановцы в белых балахонах бегут по полю за чернокожим футболистом. Сижу, тихо улыбаюсь. Знаете, как отвлекает….

Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.

Пример 6

Найти общее решение системы линейных уравнений.

Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.

Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.

Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.

В общее решение системы иногда может входить константа (или константы), например: . Здесь одна из базисных переменных равна постоянному числу: . В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.

Редко, но встречаются системы, в которых количество уравнений больше количества переменных . Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.

Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:

где a ij – коэффициенты, а b i – постоянные.

Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Для системы линейных уравнений матрица

А = называется матрицей системы, а матрица

А * = называется расширенной матрицей системы

Определение. Если b 1 , b 2 , …,b m = 0 , то система называется однородной. Замечание. Однородная система всегда совместна, т.к. всегда имеет нулевое решение.

Элементарные преобразования систем.

1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2. Перестановка уравнений местами.

3. Удаление из системы уравнений, являющихся тождествами для всех х .

Формулы Крамера.

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений.

Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам: x i = где D = det A , а D i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b i .

D i =

Пример. Найти решение системы уравнений:

D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

D 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

D 3 = = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.

Замечание 1. Если система однородна, т.е. b i = 0 , то при D¹0 система имеет единственное нулевое решение x 1 = x 2 = … = x n = 0.

Замечание 2. При D = 0 система имеет бесконечное множество решений.

Метод обратной матрицы.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Пусть дана система уравнений: Составим матрицы:

A = - матрица коэффициентов при переменных или матрица системы;

B = - матрица –столбец свободных членов;

X = - матрица – столбец неизвестных.

Тогда систему уравнений можно записать:A×X = B. Домножим слева обе части равенства на A -1: A -1 ×A×X = A -1 ×B, т.к. А -1 ×А = Е, то Е×Х = А -1 ×В , то справедлива следующая формула:

Х = А -1 ×В

Таким образом, для применения данного метода необходимо находить обратную матрицу.

Пример. Решить систему уравнений:

Х = , B = , A =

Найдем обратную матрицу А -1 .

D = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ обратная матрица существует.

M 11 = ; M 21 = ; M 31 = ;

M 12 = M 22 = M 32 =

M 13 = M 23 = M 33 =

A -1 = ;

Cделаем проверку:

A×A -1 =
=E.

Находим матрицу Х.

Х = = А -1 В = × = .

Получили решения системы: x =1; y = 2; z = 3.

4.Метод Гаусса .

Пусть дана система m линейных уравнений с n неизвестными:

Полагая, что в системе коэффициент a 11 отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x 1). Преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x 1 с помощью эквивалентных преобразований описанным выше способом.

В полученной системе

считая, что (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x 2 . Во вновь полученной системе

при условии оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x 3 .

Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:

1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;

2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;

3) если получается ступенчатая система коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.

Рассмотрим квадратную систему: (1)

У этой системы коэффициент a 11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x 1 не равен нулю.

Проведем следующие преобразования системы:

1) поскольку a 11 ¹0, первое уравнение оставим без изменений;

2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;

3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;

4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.

Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x 1 (это и являлось целью преобразований 1 – 4): (2)

Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы

. (3)

Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы , которую иногда называют просто матрицей системы .

Системе (2) соответствует расширенная матрица

Преобразуем эту матрицу следующим образом:

1) первые две строки оставим без изменения, поскольку элемент a 22 не равен нулю;

2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;

3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.

В результате получится матрица, соответствующая системе, у которой неизвестная x 1 исключена из всех уравнений, кроме первого, а неизвестная x 2 - из всех уравнений кроме первого и второго:

Теперь исключим неизвестную x 3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:

1) первые три строки оставим без изменения, так как a 33 ¹ 0;

2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой: .

Полученная матрица соответствует системе

. (4)

Из последнего уравнения этой системы получаем x 4 = 2. Подставив это значение в третье уравнение, получим x 3 = 3. Теперь из второго уравнения следует, что x 2 = 1, а из первого - x 1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x 4 , затем x 3 и т. д.).

Определение: Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей .

Матрица коэффициентов системы (4) – треугольная матрица.

Замечание: Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.

Рассмотрим другой пример: . (5)

Проведем следующие преобразования расширенной матрицы системы:

1) первую строку оставим без изменения;

2) вместо второй строки запишем разность между второй строкой и удвоенной первой;

3) вместо третьей строки запишем разность между третьей строкой и утроенной первой;

4) четвертую строку заменим разностью между четвертой и первой;

5) пятую строку заменим разностью пятой строки и удвоенной первой.

В результате преобразований получим матрицу

Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:

Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x 3 в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу

Каждая из двух последних строк этой матрицы соответствует уравнению 0x 1 +0x 2 +0x 3 +0x 4 +0x 5 = 0. Это уравнение удовлетворяется любым набором чисел x 1 , x 2 , ¼, x 5 , и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида

. (6)

Последняя строка этой матрицы соответствует уравнению
x 3 – 2x 4 + 3x 5 = –4. Если неизвестным x 4 и x 5 придать произвольные значения: x 4 = С 1 ; x 5 = С 2 , то из последнего уравнения системы, соответствующей матрице (6), получим x 3 = –4 + 2С 1 – 3С 2 . Подставив выражения x 3 , x 4 , и x 5 во второе уравнение той же системы, получим x 2 = –3 + 2С 1 – 2С 2 . Теперь из первого уравнения можно получить x 1 = 4 – С 1 + С 2 . Окончательно решение системы представляется в виде .

Рассмотрим прямоугольную матрицу A , у которой число столбцов m больше, чем число строк n . Такую матрицу A назовем ступенчатой .

Очевидно, что матрица (6) - ступенчатая матрица.

Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду

0x 1 + 0x 2 + ¼0x n = b j (b j ¹ 0),

то система несовместна или противоречива, так как ни один набор чисел x 1 , x 2 , ¼, x n не удовлетворяет этому уравнению.

Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к ступенчатому виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений .

В последней системе можно получить все решения, придавая конкретные числовые значения параметрам С 1 и С 2 .

Определение: Те переменные, коэффициенты при которых стоят на главной диагонали ступенчатой матрицы (это значит, что эти коэффициенты отличны от нуля), называются основными . В рассмотренном выше примере это неизвестные x 1 , x 2 , x 3 . Остальные переменные называются неосновными. В рассмотренном выше примере это переменные x 4 , и x 5 . Неосновным переменным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.

Основные переменные единственным образом выражаются через неосновные переменные.

Определение: Если неосновным переменным приданы конкретные числовые значения и через них выражены основные переменные, то полученное решение называется частным решением .

Определение: Если неосновные переменные выражены через параметры, то получается решение, которое называется общим решением.

Определение: Если всем неосновным переменным приданы нулевые значения, то полученное решение называется базисным .

Замечание: Одну и ту же систему иногда можно привести к разным наборам основных переменных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда основными будут переменные x 1 , x 2 , x 4 , а неосновными – x 3 и x 5 .

Определение: Если получены два различных набора основных переменных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число переменных, называемое рангом системы.

Рассмотрим еще одну систему, имеющую бесконечно много решений: .

Проведем преобразование расширенной матрицы системы по методу Гаусса:

Как видно, мы не получили ступенчатой матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы: .

Эта матрица уже является ступенчатой. У соответствующей ей системы две неосновные переменные – x 3 , x 5 и три основные – x 1 , x 2 , x 4 . Решение исходной системы представляется в следующем виде:

Приведем пример системы, не имеющей решения:

Преобразуем матрицу системы по методу Гаусса:

Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x 1 + 0x 2 + 0x 3 = 1 . Следовательно, исходная система несовместна.

Лекция № 3.

Тема: Векторы. Скалярное, векторное и смешанное произведение векторов

1. Понятие вектора. Коллинарность, ортогональность и компланарность векторов.

2. Линейная операция над векторами.

3. Скалярное произведение векторов и его применение

4. Векторное произведение векторов и его применение

5. Смешанное произведение векторов и его применение

1. Понятие вектора.Коллинарность, ортогональность и компланарность векторов.

Определение: Вектором называется направленный отрезок с начальной точкой А и конечной точкой В.

Обозначение: , ,

Определение: Длиной или модулем вектора вектора называется число, равное длине отрезка АВ, изображающего вектор.

Определение: Вектор называется нулевым, если начало и конец вектора совпадают.

Определение: Вектор единичной длины называется единичным. Определение: Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( || ).

Замечание:

1.Коллинеарные векторы могут быть направлены одинаково или противоположно.

2. Нулевой вектор считается коллинеарным любому вектору.

Определение: Два вектора называются равными, если они коллинеарные,

одинаково направлены и имеют одинаковые длины ( = )

Системой m линейных уравнений с n неизвестными называется система вида

где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 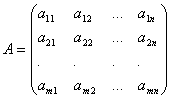, которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.

Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов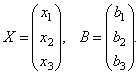

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

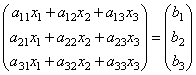или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .

Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

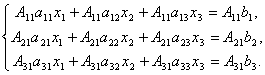
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

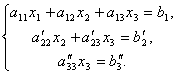
Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.